Você provavelmente usa folhas sulfite todos os dias. E se já explorou um pouco as configurações do Microsoft Word ou outro editor de texto sabe que ela tem uma medida muito estranha para um objeto tão comum: 21 centímetros de largura por 29,7 de altura. Não pode ser 20 cm de largura. Não pode ser 30 cm de altura. Quem inventou esse número e porque raios ele tem tantas casas decimais?
Bom, se você já visitou qualquer papelaria, sabe que uma folha A4, nome oficial da Folha Sulfite Padrão, é metade de um A3, que é metade de um A2, que é metade de um A1 que é metade de um A0.

Até aí, pode parecer um pouco óbvio. Mas o tamanho do A0 também não foi inventado do nada, por capricho de alguém.

O A0 tem, precisamente, a área de um metro quadrado. E o metro também tem raízes bem reais: ele foi definido como uma fração da circunferência da Terra.

Mas espera um pouco. Um metro quadrado é…. quadrado. A folha A0 é retangular.
Isso também tem motivo.
O comprimento dos seu lados é precisamente calculado para que, toda a vez que você dobre a folha no meio, obtenha duas metades iguais, nas quais a proporção entre os lados é a mesma do que na folha antiga.
Um quadrado jamais se encaixaria nessa ideia: quando você dobra um quadrado no meio obtém dois retângulos.
Essa regra não é só pedantismo matemático. Ela é bastante prática. Se a A0 fosse quadrada, você teria um problemão se quisesse, por exemplo, escanear um desenho feito em A3 e imprimi-lo em casa em uma A4. Sobraria muito papel em branco na folha, ou a imagem ficaria muito pequena. Para preencher tudo, seria precido distorcer todo o desenho.
Pensando na necessidade de reproduzir informação em diferentes tamanhos é que os papeis de A0 a A5 foram pensados para manter a mesma razão entre os lados toda a vez que você faça a dobra no meio.
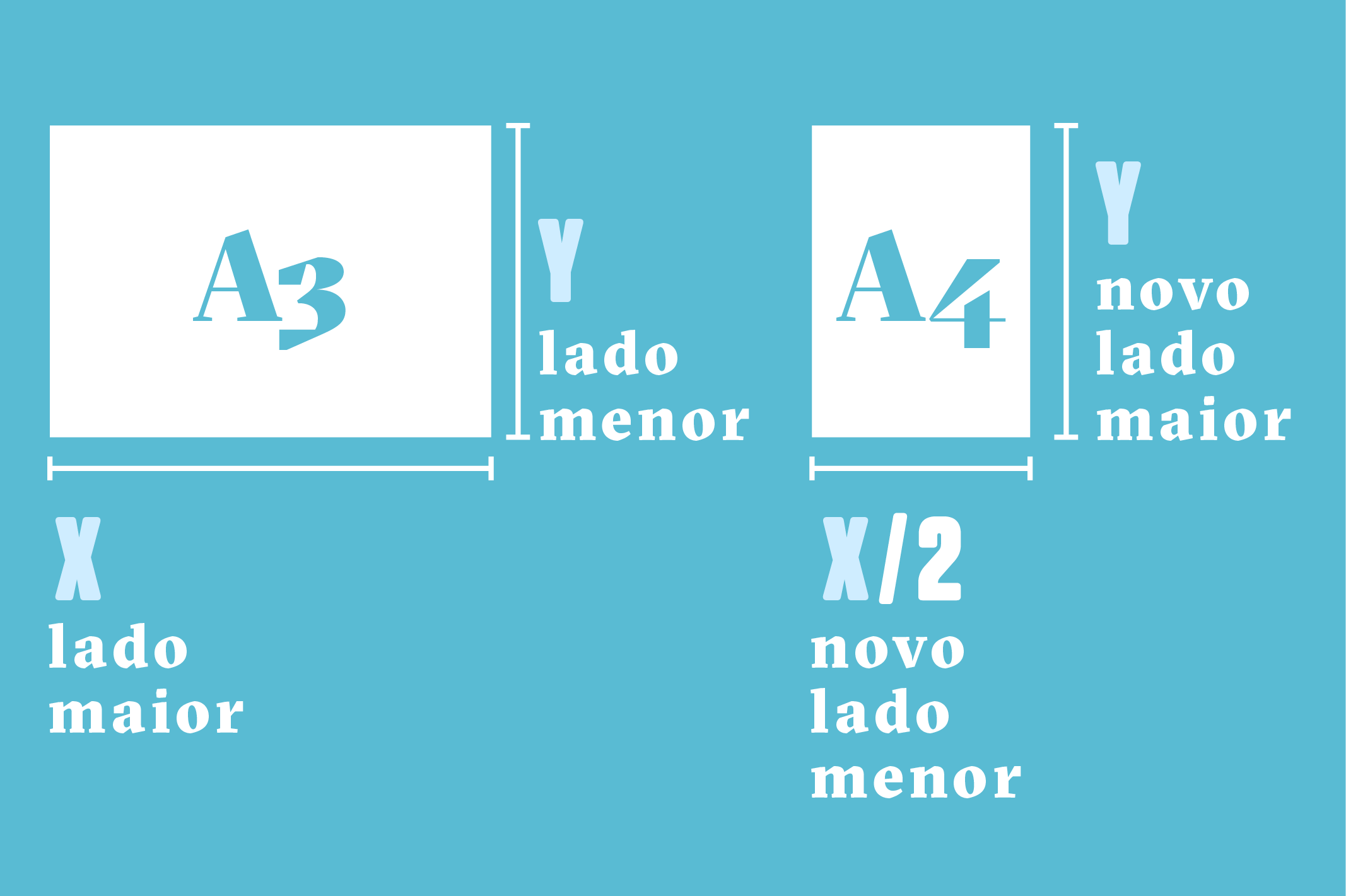
Mas achar essa proporção que se mantém é mais complicado que parece. É mais complicado do que parece. Toda a vez que você dobra uma folha sulfite no meio, o lado maior se torna o menor, dividido pela metade. Mas o outro lado fica com o mesmo tamanho. Como fazer com que a relação entre os tamanhos seja sempre a mesma?

Essa é a única proporção que permite a mesma relação entre o tamanho dos lados na dobradura de A0 = 2 A1 = 4 A2 = 8 A3 = 16 A 4 = 24 A5.
Se você fizer a conta com o tamanho do A4, o lado menor (21 cm) vezes raiz de 2 (1,4142) vai ter como resultado 29,6982. Ou seja, a estranhíssima medida de 29,7 é um arrendondamento, para facilitar. Mais uma prova de que, no campo dá matemática, as coisas geralmente são mais complicadas do que parecem.
autores: Ana Carolina Leonardi e Thales Molina
fonte: Revista Superinteressante





